微分方程的解法（解方程与解微分方程）

“=”，即等号，是我们再熟悉不过的数学符号了，相较与“>”或“<”号，等号的使用似乎更为普遍，因为，等号说明的不仅仅是数量的相等，还可以是表示两样“东西”完全一样。

比如，我们说

左边看上去完全和“1”不是一码事，为什么用等号呢？原来，这里不管x取什么值，左边的值都等于1，所以左右其实是一个东西。

有的时候，不是所有的x都使得等式成立，比如下面这个等式，不是对所有的x都成立，我们想找出使得等式成立的x的值，这就叫解方程。

我们知道，满足这个等式的x有两个值，叫做这个方程的两个解，分别是和。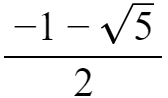

再比如说，对于

这里的y是一个关于x的函数，但不是所有的函数y都使得上面的等式成立，那我们就不禁要问了，当y是个什么函数时才有等号成立呢？这就是解微分方程了。这里，使得这个微分方程成立的y的解有无穷多个，它们的形式却只有一个，即

解方程与解微分方程是门大学问，有的时候，找出所有的解来（有公式求解）并不是件容易的事情（想一想你都会解哪些方程和微分方程？），但我们也有找到一个近似解（有的时候能找到准确解）的数值方法。

如果方程

里的f(x)是一个连续函数，我们可以用利用连续性来寻找近似解：

首先，如果不容易找到解的话，我们先要找到两个点，一个点处函数值f(x)为正值，一个点为负值，如果实在找不到一正一负的点，可能方程无解。

然后，根据连续性，两点之间必有至少一个解，我们只要在两点之间再取一个点，看看是正还是负（是零就找到解啦），如果是正（负）的，就和前面的负（正）的点从新组合成一对点，新的点对的两点之间的距离比之前更小，同样，新的两点间也存在至少一个解。

这样一直下去，我们有希望找到准确的解，也一定会让包含解的区间变得越来越小，从而得到一个很好的近似解。

解微分方程的时候，如果微分方程可以写成

的形式，但我们并不容易解出y的形式来，我们可以利用方程的slope field（由显示斜率的小线段构成）来找出一个y的近似解的函数曲线图来。比如下图演示的是如何对的slope field里画一个过点（0，0）的满足该微分方程的解：

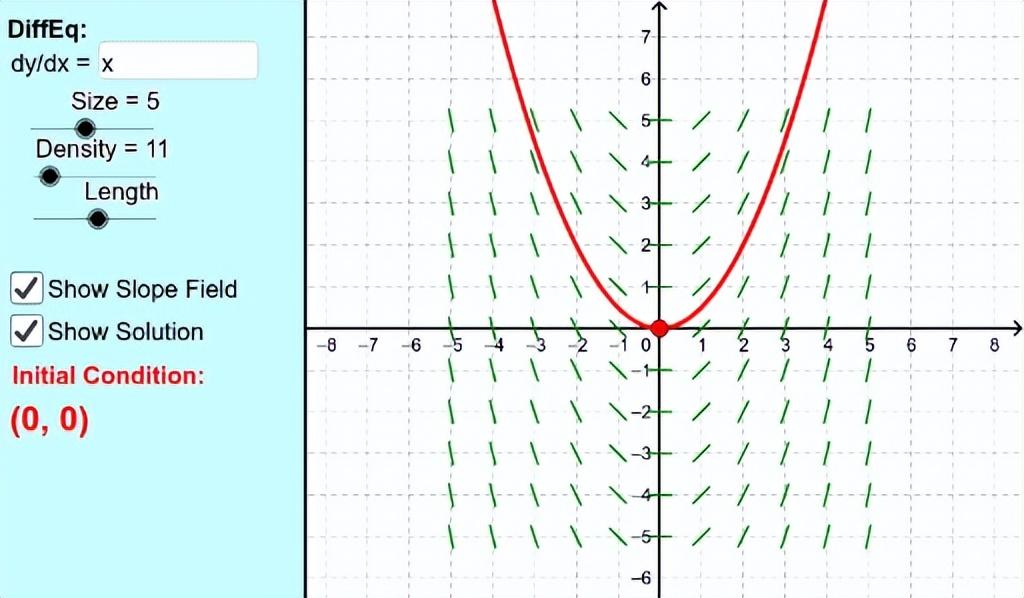
slope field

我们只要沿着小绿线段所指的方向来画一条光滑的曲线就可以了。

以上说的是一类方程和微分方程的近似解法，也是经常遇到的，其实要真正用好方程与微分方程，除了要会解比较常见的方程和微分方程，也要会根据实际问题列出对应的方程或微分方程。

在中小学阶段，我们学的是列方程与解方程。

大学微积分里，我们开始学习列微分方程与解微分方程。这也是我们解决应用问题能力的一个拓展。这里举一个简单的例子——人口增长模型。

我们经常听到说，人口呈指数级增长，这是为什么呢？是人特别能生的缘故么？还是其他什么原因？

其实，人口数量的净增长，是和人口总数成比例的，这个道理好懂。因为每年十亿人的国家显然比一千万人口的国家净增长的人要多得多。所以，我们可以列一个微分方程。设，人口在时间为t的时候，数量为P(t)， 而每年人口的净增长数和总人数的比例是k, 人口的初始数量是，则

我们可以通过“变量分离法”来解这个方程，得到

即使你不会用解微分方程，只是会一些求导数的技巧，你也可以验证这个关于t的指数函数满足这个微分方程与初始条件，所以它确实是这个微分方程的解。而且这是唯一的解。所以，人口的增长是呈指数增长的。

只是，现实的环境资源有限，人口数量过大会导致生存环境恶化，使得人口会稳定到一个数量不再增长，所以这个模型也只是能模拟在生存资源极其充足的情况下的人口增长情况。

好了，就讲到这儿，如果你不是对数学特别喜欢钻研，你能了解到一点方程和微分方程是什么，怎么解，怎么用，也就很不错啦！